

Our tool can also compute the sum of your sequence: all of it or a final portion. You can change the starting and final terms according to your needs. By default, the calculator displays the first five terms of your sequence.Based on that, the calculator determines the whole of your geometric sequence. the common ratio and some n th term or.the common ratio and the first term of the sequence.First, tell us what you know about your sequence by picking the value of the Type:.Here's a brief description of how the calculator is structured:
#Arithmetic explicit formula how to
Now that you know what a geometric sequence is and how to write one in both the recursive and explicit formula, it is time to apply your knowledge and calculate some stuff! With our tool, you can calculate all properties of geometric sequences, such as the common ratio, the initial term, the n-th last term, etc. But if we consider only the numbers 6, 12, 24 the GCF would be 6 and the LCM would be 24. For example, in the sequence 3, 6, 12, 24, 48 the GCF is 3 and the LCM would be 48. Conversely, the LCM is just the biggest of the numbers in the sequence. This means that the GCF (see GCF calculator) is simply the smallest number in the sequence. Indeed, what it is related to is the [greatest common factor (GFC) and lowest common multiplier (LCM) since all the numbers share a GCF or a LCM if the first number is an integer. First of all, we need to understand that even though the geometric progression is made up by constantly multiplying numbers by a factor, this is not related to the factorial (see factorial calculator). We also include a couple of geometric sequence examples.īefore we dissect the definition properly, it's important to clarify a few things to avoid confusion. If you are struggling to understand what a geometric sequences is, don't fret! We will explain what this means in more simple terms later on, and take a look at the recursive and explicit formula for a geometric sequence. Problem 4: Find the explicit formula of the following geometric sequence 4, 8, 16, 32, 64,…Īnswer: 1) an = an-1 + 10 where a1 = 24 2) an = an-1 * 4 where a1 = 9 3) an = 4n + 5 4) an = 4 * 2n – 1.The geometric sequence definition is that a collection of numbers, in which all but the first one, are obtained by multiplying the previous one by a fixed, non-zero number called the common ratio.
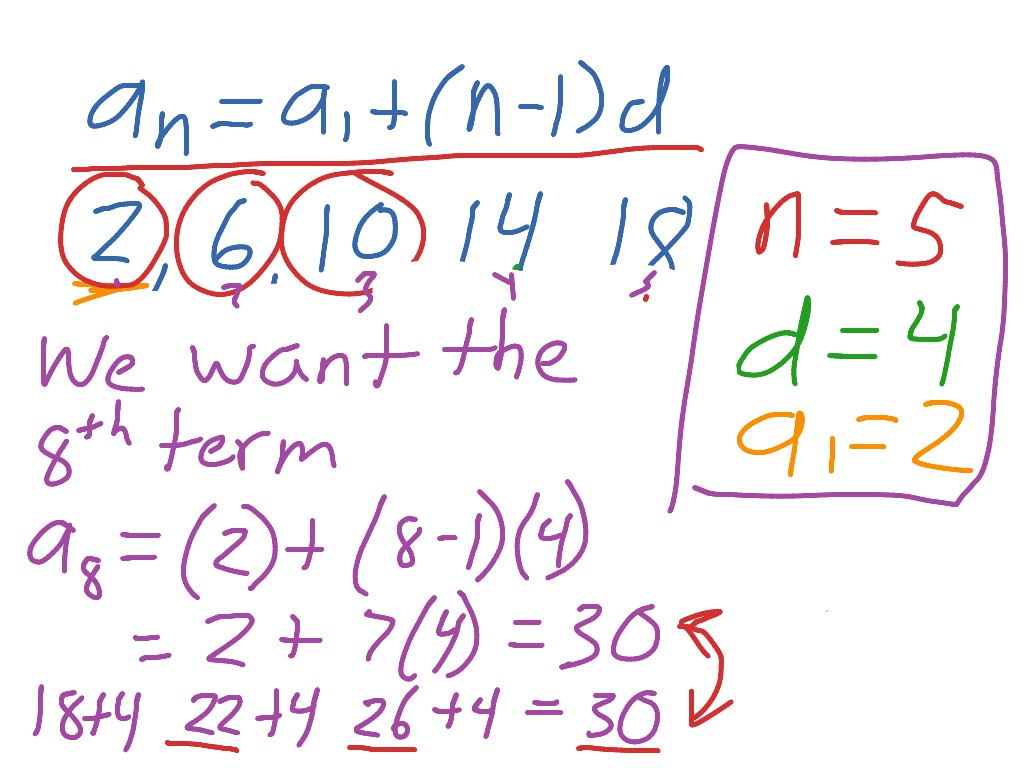
Problem 3: Find the explicit formula of the following arithmetic sequence 9, 13, 17, 20, 23, 26, 29,… Problem 2: First term of the sequence a1 = 9, common ratio r = 4, find the recursive formula of the geometric sequence.

Problem 1: First term of the sequence a1 = 24, common difference d = 10, find the recursive formula of the arithmetic sequence. Recursive and Explicit Formulas – Practice Problems Therefore, explicit formula of the given geometric sequence is an = 3 * 4n – 1. Therefore, explicit formula of the given arithmetic sequence is an = 6n + 5.Įxample 4: Find the explicit formula of the following geometric sequence 3, 12, 36, 108, 432,…įirst term a1 = 3, common ratio r = `12/3` = 4 Use nth term formula to find the explicit formula Therefore, recursive formula of the geometric sequence is of the an = an-1 * 3 where a1 = 12.Įxample 3: Find the explicit formula of the following arithmetic sequence 11, 17, 23, 29, 35, 41, 47,…įirst term a1 = 11, common difference d = 17 – 11 = 6 Therefore, recursive formula of the arithmetic sequence is of the an = an-1 + 14 where a1 = 28.Įxample 2: First term of the sequence a1 = 12, common ratio r = 3, find the recursive formula of the geometric sequence. Recursive and Explicit Formulas – Example ProblemsĮxample 1: First term of the sequence a1 = 28, common difference d = 14, find the recursive formula of the arithmetic sequence.įirst term a1 = 28, common difference d = 14. Explicit formula is used to find the nth term of the sequence using one or more preceding terms of the sequence. Recursive formula is used to find the next term of the sequence using one or more preceding terms of the sequence. Geometric sequence is a sequence of numbers such that the ratio between two successive members of the sequence is a constant. Arithmetic sequence is a sequence of numbers such that the difference between two successive members of the sequence is a constant.


 0 kommentar(er)
0 kommentar(er)
